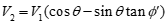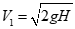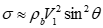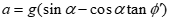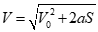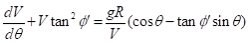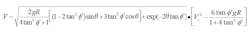Transfer chute fundamentals and snowboarding

I am a native of Colorado, and I enjoy skiing. Recently, I thought I’d give snowboarding a try, and my nephew was eager to teach me. It was a disaster! My nephew reminded me that I used to skateboard when I was in college, and he wondered why snowboarding was more challenging for me. I gave the problem some thought, and when we returned to the lodge, I used my knowledge of how to design transfer chutes to explain the differences between skateboarding and snowboarding. 

A transfer chute is used to control and direct the movement of a bulk solid from a delivery point to a destination. The chute must be sufficiently steep, and its friction must be low enough to permit the material to slide and fully clean off of the chute. 

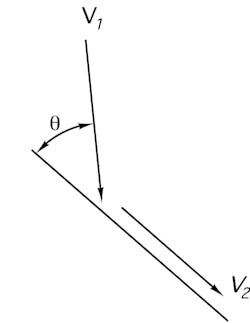
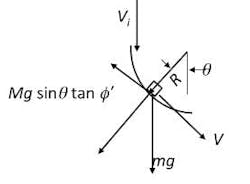
Referring to Figure 1, the velocity of a stream of particles (assuming no bouncing) after impacting a chute V₂, relative to its velocity before impact V₁, is:

where θ is the impact angle and ϕ’ is the wall friction angle. The wall friction angle ϕ’ is related to the friction coefficient m by:

Wall friction is measured by placing a sample of powder inside a cell and then recording the force required to slide the powder along a coupon of wall material¹. The shear force is measured over a range of normal loads.

If the particles fall freely when they are dropped onto the chute, their velocity before impact V₁ is its free-fall velocity:

where H is the drop height.

If the sum of ϕ’ and θ equals 90 degrees, the value of V₂ in Equation 1 is equal to zero and the bulk material will not slide on the chute surface. The angle of inclination must therefore be greater than the material’s wall friction angle to ensure flow.

To determine the minimum chute angle required to overcome adhesion at impact, chute tests are performed². To conduct a chute test, a sample of the bulk material is loaded onto a wall coupon and a load representing the impact pressure is briefly applied and then removed. The impact pressure σ is approximately equal to:

The coupon is inclined until the sample just starts to slide, and the angle of inclination is recorded. In the design of a transfer chute, a safety factor of 5 degrees is usually applied to this value to ensure clean-off. If a slope of 10 degrees greater than the minimum is used, the chute will remain cleaner than Doris Day’s greatest hits album.

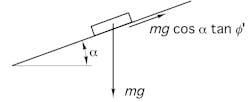
While sliding on a straight surface, the particles will accelerate or decelerate, depending on the relative values of the chute angle α measured from horizontal and the wall friction angle ϕ’ (see Figure 2):

where a is the acceleration.

With a little effort, Equation 5 can be rewritten as:

Equation 6 shows that, for the acceleration to be positive, the angle of inclination must be greater than the material’s wall friction angle.

If the chute cross section does not decrease along a distance S on the chute surface, Equation 6 can be integrated to give the stream velocity V:

where V₀ is the material’s velocity at the chute entrance. 

An obvious goal in the design of a transfer chute is that the velocity of the material is never equal to zero. Having a negative acceleration is permissible and in fact is frequently desirable as too high a velocity can lead to dust formation and avalanching. Often a chute is fabricated in sections where the initial section is steep enough to ensure flow after impact, followed by sections that have less inclination. If the material is to land on a belt conveyor at the chute’s exit, the velocity of the material stream should be in the direction of and equal to or greater than the belt velocity.

When the velocity of the material stream changes as the material passes through a chute, the stream’s cross-sectional area will change. To prevent flow stoppages, the chute should be sized such that it is no more than about one-third to one-half full where the material is at minimum velocity.

While chutes can be fabricated and installed in rectangular sections, designing a chute with curved surfaces has advantages. Chutes fabricated from cylindrical pipes or having rounded surfaces control the stream effectively, as they can be used to center the material and allow its momentum to keep the chute clean. 

Flow onto a curved chute is illustrated in Figure 3. Dynamic equilibrium of forces gives:

where R is the radius of the curved surface and θ is the angular coordinate. For a constant radius and wall friction angle, Equation 8 has an analytical solution³:

When designing chutes with complicated geometries or when the solids fly off a belt before they enter the chute, Discrete Element Method (DEM) models should be used. (Refer to Reference 4 at the end of this article for an overview of DEM modeling.)

To reduce the solids impact pressure, free fall height and sudden changes in the direction of material flow should be minimized. High impact can result in attrition, abrasive wear, and generation of dust. Since impact pressure is proportional to sin²θ and V₁², reducing the impact angle and drop height reduces wear. In addition, lengthy drop heights can exacerbate segregation due to differences in particle velocities.

Attrition of friable particles is most likely to occur at impact points where the impact pressures are high. Therefore, attrition can be reduced by minimizing the impact angle, maintaining a constant stream velocity, and ensuring that the flowing stream is concentrated and remains in contact with the chute surface.

To return to my snowboarding adventure, I pointed out that Equation 6 had two terms: α, which is related to the slope, and ϕ’, which is related to friction. When I was on a skateboard, the slope was shallow, and the friction was high, so my acceleration was manageable. On a snowboard, however, the slope is high, and the friction is low. Consequently, my acceleration could be quite high. In fact, the only time my acceleration wasn’t high was when I fell, because the friction between the seat of my pants and the snow was significantly greater than the friction between my snowboard and the snow, so my acceleration was negative.

While I still cannot snowboard, at least my nephew now understands how to design transfer chutes for bulk solids.

References

1.     Mehos, G., “Designing Hoppers, Bins, and Silos for Reliable Flow,” Chem. Engr. Progress, 114, 4 (Apr. 2018).

2.     Stuart, D. and T. Royal. “Design Principles for Chutes to Handle Bulk Solids,” Bulk Solids Handling, 12, 3 (Mar. 1992).

3.     Frittella, A. and A. Smit, “Chute Design Essentials — How to Design and Implement Chutes in Bulk Solids Handling Systems,” Bulk Solids Handling, 35, 6, 447 (2015).

4.     Bharadwaj, R. “Using DEM to Solve Bulk Material Handling Problems,” Chem. Engr. Prog., 108, 9 (Sept. 2012).